Неевклидова геометрия

История неевклидовой геометрии слишком сложна, чтобы описывать ее во всех подробностях, но мы можем резюмировать результаты, полученные благодаря усилиям ее первопроходцев. Была установлена глубокая связь между тремя случаями, отмеченными Саккери, Ламбертом, Гауссом, Бойяи и Лобачевским. Их всех объединяет идея кривизны. Неевклидова геометрия – на самом деле естественная геометрия криволинейной поверхности. Если поверхность имеет положительную кривизну, как сфера, мы имеем дело с тупым углом. Это долгое время отвергалось из-за слишком очевидных отличий сферической геометрии от евклидовой – например, потому что здесь любые две линии, т. е. большие круги, чьи центры совпадают с центром Земли, встречаются в двух точках, а не в одной, как мы ожидаем от евклидовых прямых.

Теперь нам ясно, что эти возражения необоснованны. Если мы отождествим в одну точку диаметрально противоположные точки на сфере – т. е. примем, что они идентичны, – то линии (большие круги) всё равно будут иметь смысл: если точка лежит на большом круге, на нем же будет лежать и диаметрально противоположная ей. С таким определением практически все геометрические свойства остаются неизменными, но теперь линии встречаются в одной точке. Топологически в результате мы получаем проективную плоскость, хотя задействованный здесь подход – далеко не общепринятая проективная геометрия. Сейчас мы называем ее эллиптической геометрией, и она так же востребована, как геометрия Евклида.

Если поверхность имеет отрицательную кривизну, как седло, мы переходим к случаю с острым углом. Полученная в результате геометрия называется гиперболической. Она имеет множество занимательных особенностей, отличающих ее от евклидовой.

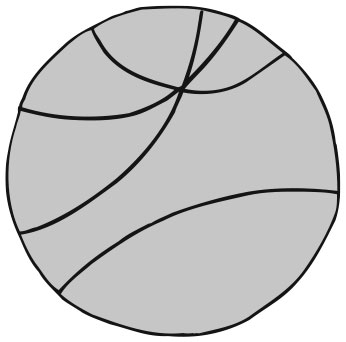
Модель Пуанкаре гиперболической геометрии делает ее более ясной: через точку, не лежащую на данной прямой, проходит бесконечно много параллельных (не пересекающих ее) линий

Если кривизна поверхности нулевая, как у евклидовой плоскости, то мы попадаем в область евклидовой геометрии. Все три геометрии удовлетворяют всем аксиомам Евклида, за исключением пятого постулата. Решение Евклида включить его было оправданным.

Эти различные геометрии могут быть выражены самыми разными способами. И здесь особенно многогранна гиперболическая геометрия. В одной модели соответствующее пространство может оказаться верхней комплексной полуплоскостью, без вещественной оси и всего, что ниже ее. Линия является полуокружностью, встречающейся с вещественной осью под прямыми углами. Топологически данное пространство есть не что иное, как плоскость, а его линии тождествены обычным. Изгиб линий отражает отрицательную кривизну гиперболического пространства.

Во второй модели гиперболической геометрии, исследованной Пуанкаре, пространство заключено внутри круга, не включает его границы, а линии являются дугами окружностей и пересекают границу под прямыми углами. И снова данный вид геометрии отражает кривизну пространства. Художник Мауриц Эшер создал много картин, основанных на этой модели гиперболической геометрии, с которой его познакомил канадский ученый Коксетер.

Обе модели затрагивают глубинные связи между гиперболической геометрией и комплексным анализом. Эти связи относятся к основным группам преобразований комплексной плоскости. Согласно «Эрлангенской программе» Феликса Клейна, гиперболическая геометрия является геометрией инвариантов таких преобразований. Другой класс трансформаций, так называемые преобразования Мёбиуса, в свою очередь, вводят в игру эллиптическую геометрию.